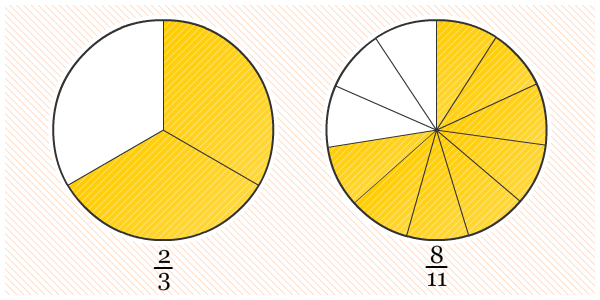
Dengan bantuan gambar di atas, kita dapat melihat dengan mudah bahwa 8/11 lebih besar dari 2/3, atau dapat dituliskan 8/11 > 2/3. Sekarang mari kita lihat posisi kedua pecahan tersebut pada garis bilangan.
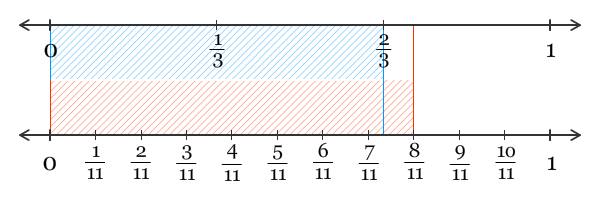
Dari garis bilangan tersebut, kita dapat memperoleh bahwa 8/11 berada di kanan 2/3. Hal ini merupakan bukti lain bahwa 8/11 lebih besar dari 2/3. Selain dengan menggunakan gambar dan garis bilangan, apakah ada cara lain untuk membandingkan dua pecahan?
Mengurutkan Pecahan dengan Menyamakan Penyebut
Membandingkan pecahan dapat dilakukan dengan menyamakan penyebutnya. Penyebut dari pecahan-pecahan yang belum sama, dapat disamakan dengan menggantinya dengan faktor persekutuan penyebut pecahan-pecahan tersebut.
Misalkan kita akan membandingkan dua pecahan sebelumnya, yaitu 8/11 dan 2/3. Faktor persekutuan dari 11 dan 3 di antaranya adalah 33, 66, 99, dan 132. Kita ambil saja faktor persekutuan yang terkecil, atau disebut KPK, yaitu 33. Sehingga,
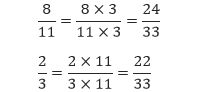
Karena 24 bagian dari 33 lebih besar daripada 22 bagian dari 33, maka
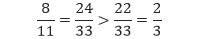
Setelah dapat membandingkan dua pecahan, sekarang kita akan berlatih untuk mengurutkan beberapa pecahan. Misalkan diberikan pecahan-pecahan 1/3, 2/5, 4/15, 5/12, dan 5/6. Dapatkah kamu mengurutkan pecahan-pecahan tersebut dari yang terkecil ke terbesar?
Sebelum mengurutkan pecahan-pecahan tersebut, kita harus membandingkan pecahan-pecahan tersebut dengan menyamakan penyebutnya. KPK dari 3, 5, 15, 12, dan 6 adalah 60. Sehingga,
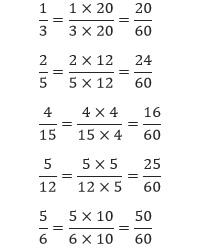
Setelah menyamakan penyebut-penyebutnya, kita tentu mudah untuk mengurutkannya. Urutan pecahan-pecahan dari yang terkecil ke terbesar adalah,
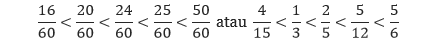
Untuk mengurutkan pecahan dengan menyamakan penyebutnya terlebih dahulu, apa yang perlu diperhatikan?
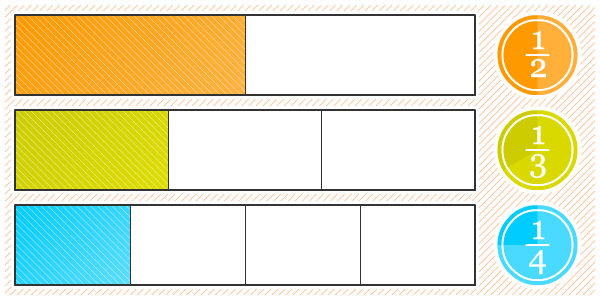
Agar kalian lebih memahaminya, perhatikan gambar berikut!Apabila dua pecahan memiliki penyebut yang sama, pecahan yang memiliki pembilang yang lebih besar, nilainya lebih besar daripada pecahan yang pembilangnya lebih kecil.
Selain dengan menyamakan penyebutnya, kita dapat mengurutkan beberapa pecahan dengan menyamakan pembilangnya.
Mengurutkan Pecahan dengan Menyamakan Pembilang
Sebelum kita mulai mengurutkan beberapa pecahan dengan menyamakan pembilangnya, mari kita tinjau pecahan-pecahan yang pembilangnya sama berikut.
Dari ketiga contoh pecahan di atas, apa yang dapat kita peroleh?
Agar kamu mudah mengingat pernyataan di atas, kamu dapat memperhatikan gambar berikut.Apabila dua pecahan memiliki pembilang yang sama, maka pecahan yang penyebutnya lebih besar, nilainya lebih kecil daripada pecahan yang penyebutnya lebih kecil.
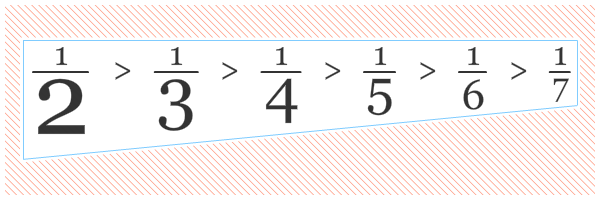
Selanjutnya mari kita urutkan pecahan-pecahan 1/2, 3/5, 2/3, 4/7, dan 5/9 dari yang terbesar ke terkecil. KPK dari 1, 2, 3, 4, dan 5 adalah 60. Sehingga,
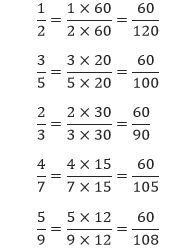
Setelah menyamakan pembilang-pembilangnya, kita tentu mudah untuk mengurutkannya. Urutan pecahan-pecahan dari yang terbesar ke terkecil adalah,
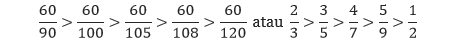
Semoga bermanfaat,
http://yos3prens.wordpress.com/2013/05/31/mengurutkan-pecahan/



 :
:


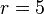

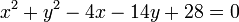
 dan menyinggung garis
dan menyinggung garis 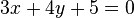 !
!
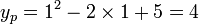


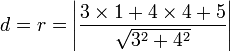





 terhadap lingkaran
terhadap lingkaran 
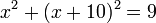



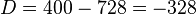
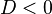 , maka garis berada di luar lingkaran.
, maka garis berada di luar lingkaran. terletak di luar lingkaran
terletak di luar lingkaran 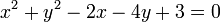 !
!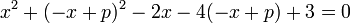
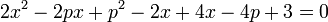

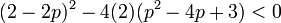



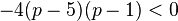
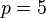 atau
atau 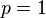
 atau
atau 
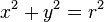 , maka persamaan garis singgungnya:
, maka persamaan garis singgungnya:
 , maka persamaan garis singgungnya:
, maka persamaan garis singgungnya: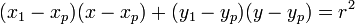

 atau
atau 